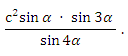А1. В треугольнике АВС стороны АВ = 4 см, ВС = 5 см, BD - биссектриса. Найдите отношение площади треугольника ABD к площади треугольника АВС.

  1) 4 : 5

  2) 5 : 9

  3) 4 : 9

  4) 16 : 81

  Ответ: 3.

  А2. В треугольнике АВС углы А = 45^°, С = 15^°, сторона ВС = 4√6. Найдите длину стороны АС.

  1) 12

  2) 8

  3) 6√3

  4) 8√2

  Ответ: 1.

  А3. В равнобедренном треугольнике АВС (АВ = ВС) угол А = 30^° и АС = 8√3. Найдите диаметр окружности, описанной около треугольника АВС.

  1) 8

  2) 16

  3) 12√3

  4) 10√2

  Ответ: 2.

  В1. В окружность радиуса 6√3 с центром в точке О вписан треугольник АВС, в котором угол В = 30^°. Найдите радиус окружности, описанной около треугольника АОС.

  Ответ: 6.

  В2. В равнобедренном треугольнике АВС (АВ = ВС) задано: угол А = α, АС = с, АЕ - биссектриса. Найдите длину АЕ.

  Ответ:

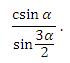
  С1. В параллелограмме ABCD диагональ АС разбивает угол С на два угла: α и 3α, АС = с. Найдите площадь параллелограмма ABCD.

  Ответ: