А1. Определите координаты центра С и радиус r окружности, заданной уравнением
(х − 3)2 + (у + 1)2 = 16.
1) С (−3; 1), r = 16
2) C (−3; 1), r = 4
3) C (3; −1), r = 16
4) C (3; −1), r = 4
Ответ: 4.
А2. Найдите координаты точек А и В пересечения прямой, заданной уравнением 2х − 3у − 12 = 0, с осями координат.
1) А (−4; 0), В (6; 0)
2) А (6; 0), В (0; −4)
3) А (−6; 0), В (0; 4)
4) А (4; 0), В (−6; 0)
Ответ: 2.
А3. Прямая, заданная уравнением 4х + by − 6 = 0, проходит через точку А (3; 2). Найдите число b.
1) b = −2
2) b = 2
3) b = 3
4) b = −3
Ответ: 4.
В1. Напишите уравнение окружности с центром в точке С (−3; −4), если эта окружность касается оси ординат.
Ответ: (х + 3)2 + (у + 4)2 = 9.
В2. Прямая проходит через точки А (−2; −1) и В (1; 1). Найдите площадь треугольника, ограниченного этой прямой и осями координат.
Ответ: 1/12.
С1. Напишите уравнение окружности, вписанной в ромб с диагоналями 10 и 12, если известно, что его диагонали лежат на осях координат.
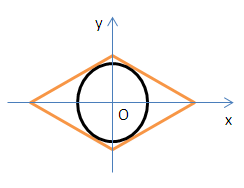
Ответ: х2 + у2 = 900/61.

