ИТОГОВЫЙ ТЕСТ ПО ТЕМЕ:

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ВАРИАНТ 1

 

  А1. В треугольнике АВС угол С равен 90^°, ВС = 28 см, синус угла В равен 3/5. Найдите длину стороны АВ.

  1) 140/3 см

  2) 30 см

  3) 35 см

  4) 40 см

  Ответ: 3.

 

  А2. Известно, что sinα · cosα = 1/4. Найдите величину sinα + cosα.

  1) 1/3

  2) √5/2

  3) 1/2

  4) √6/2

  Ответ: 4.

 

  А3. Найдите площадь пятиугольника ABCOD (см. рис.), если диагонали прямоугольника ABCD равны 13 и угол COD = 30^°.

 

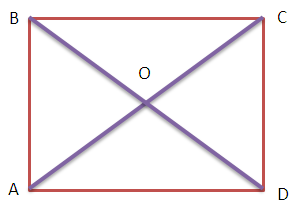
  1) 31 ¹¹/₁₆

  2) 10 ⁵/₁₆

  3) 9 ³/₈

  4) 52

  Ответ: 1.

 

  А4. Найдите радиус окружности, описанной около треугольника АВС, если АВ = 12 см, угол А = 20^°, угол В = 25^°.

  1) 8√2 см

  2) 7 см

  3) 9 см

  4) 6√2 см

  Ответ: 4.

 

  А5. Площадь треугольника АВС равна 12 см², стороны АВ и АС равны 5 см и 8 см соответственно, угол А острый. Найдите длину стороны ВС.

  1) 7 см

  2) 6 см

  3) 5 см

  4) 8 см

  Ответ: 3.

 

  А6. Векторы a и b образуют угол 45^° и

 

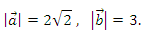
  Найдите скалярное произведение векторов

 

  1) −12

  2) 24

  3) 18

  4) −22

  Ответ: 2.

 

  В1. Найдите значение выражения:

 

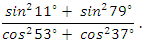
  Ответ: 1.

 

  В2. Прямая пересекает стороны АВ и АС треугольника АВС в точках Р и М соответственно. Найдите отношение площади треугольника АРМ к площади четырехугольника МСВР, если АР : РВ = 2 : 5 и АМ : МС = 1 : 4.

  Ответ: 2 : 33.

 

  В3. В треугольнике АВС дано: АВ = а, ВС = 3а, угол АВС = 90^°. Найдите длину биссектрисы BD.

  Ответ:

 

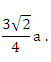
  В4. Даны векторы

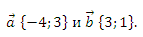
  Найдите вектор

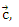
  если он удовлетворяет условиям:

 

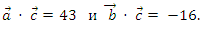
  Ответ:

 

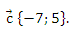
  С1. Медианы треугольника АВС, проведенные из вершин В и С, пересекаются под прямым углом. Найдите длину стороны ВС, если длина медианы треугольника, проведенной из вершины А, равна 18 см.

  Ответ: 12 см.

 

  С2. Даны векторы

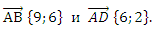
  Отрезки АВ и AD являются смежными сторонами параллелограмма. Найдите косинус угла между его диагоналями.

  Ответ: 77/85.