А1. Диагонали параллелограмма ABCD пересекаются в точке О, точка М - середина отрезка АО. Выполняется равенство

 

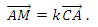
  Найдите число k.

  1) k = 3/4

  2) k = − 1/4

  3) k = − 3/4

  4) k = 1/4

  Ответ: 2.

 

  А2. Точка С принадлежит АВ и АС : АВ = 1 : 4. Найдите координаты точки С, если А (−4; 8) и В (16; 4).

  1) С (−20; 4)

  2) С (12; 6)

  3) С (−12; −6)

  4) С (1; 7)

  Ответ: 4.

 

  А3. Найдите разложение вектора

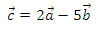
  по координатным векторам

 

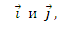
  если

  

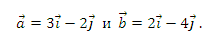
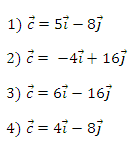
  Ответ: 2.

 

  А4. Известны координаты трех вершин прямоугольника ABCD: А (−2; −1), С (6; 3), D (6; −1). Найдите координаты вершины В.

  1) В (−2; 3)

  2) В (3; −2)

  3) В (−3; 2)

  4) В (−2; −3)

  Ответ: 1.

 

  А5. Найдите координаты центра С и радиус r окружности, заданной уравнением x² + 6x + y² − 2y = 0.

  1) C (1; 3), r = 10

  2) C (3; −1), r = √10

  3) C (−3; 1), r = √10

  4) C (−3; −1), r = 10

  Ответ: 3.

 

  А6. Найдите координаты точки пересечения прямых, заданных уравнениями 4х − 3у + 10 = 0 и х + 2у − 3 = 0.

  1) (1; 2)

  2) (−1; 2)

  3) (2; 1)

  4) (−2; 1)

  Ответ: 2.

 

  В1. Даны три последовательные вершины параллелограмма: А (1; 3), В (4; 7), С (8; 5). Найдите координаты его четвертой вершины D.

  Ответ: D (5; 1).

 

  В2. Дано разложение векторов a и b по неколлинеарным векторам m и n:

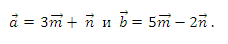
  Найдите разложение векторов m и n по векторам a и b.

  Ответ:

 

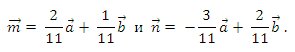
  В3. Найдите длину хорды, образующейся при пересечении окружности х² + у² = 25 и прямой х + у − 5 = 0.

  Ответ: 5√2.

 

  В4. Напишите уравнение прямой, проходящей через точки  А (−5; 3)  и В (3; 6).

  Ответ: 3х − 8у + 39 = 0.

 

  С1. Разложите вектор

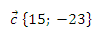
  по неколлинеарным векторам 

 

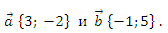
  Ответ:

 

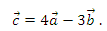
  С2. Составьте уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых, заданных уравнениями

 

 х = 0, у = 0 и 3х − 4у + 36 = 0.

 

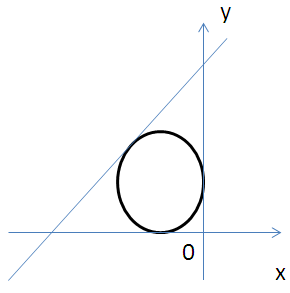
  Ответ: (х + 3)² + (у − 3)² = 9.