САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ

9 КЛАСС

ТЕМА: ТЕОРЕМА СИНУСОВ

ВАРИАНТ 1

  1. В треугольнике АВС дано: угол А = α, угол В = β, АВ = с. Найдите длину стороны АС и радиус окружности, описанной около треугольника.

  Ответ:

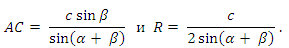
  2. В окружность радиуса R с центром О вписан треугольник АВС (угол А = α < 90^°). Вокруг треугольника ВОС описана окружность. Найдите ее радиус. (Указание: используйте формулу sin2α = 2sinαcosα).

  Ответ: R/2cosα.

  3. В треугольнике АВС дано: угол А = α, угол В = β; D - точка пересечения биссектрис. Радиус окружности, описанной около треугольника АВС, равен R. Найдите радиус окружности, проходящей через точки A, D, B.

  Ответ:

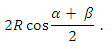
ВАРИАНТ 2

  1. В треугольнике АВС дано: угол А = α, угол В = β, ВС = а. Найдите длину стороны АС и радиус окружности, описанной около треугольника.

  Ответ:

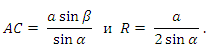
  2. В окружность радиуса R с центром О вписан треугольник АВС (угол А = α, угол В = β, α + β < 90^°). Вокруг треугольника АОВ описана окружность. Найдите ее радиус. (Указание: используйте формулу sin2α = 2sinαcosα.)

  Ответ: R/2cos(α + β).

  3. В треугольнике АВС дан угол А = α, D - точка пересечения биссектрис. Радиус окружности, описанной около треугольника АВС, равен R. Найдите радиус окружности, проходящей через точки B, D, C.

  Ответ: 2Rsin(α/2).