А1. Вектор с разложен по неколлинеарным векторам а и b следующим образом:
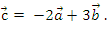
Найдите разложение вектора а по векторам b и с.
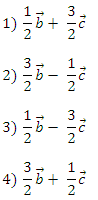
Ответ: 2.
А2. Найдите площадь круга, ограниченного окружностью, заданной уравнением
х2 + у2 + 8х − 6у + 7 = 0.
1) 7п
2) 16п
3) 20п
4) 18п
Ответ: 4.
А3. Напишите уравнение прямой, проходящей через точку А (3; −4) и перпендикулярной вектору
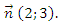
1) 2х − 3у + 4 = 0
2) 2х + 3у + 6 = 0
3) 3х − 2у + 6 = 0
4) 3х + 2у − 1 = 0
Ответ: 2.
А4. Найдите величину
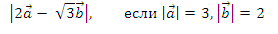
и угол между векторами а и b равен 30°.
1) 2√3
2) 6 − 2√3
3) √15
4) 2√21
Ответ: 1.
А5. Найдите отношение площадей правильных шестиугольника и четырехугольника, вписанных в одну и ту же окружность.
1) 3√3 : 2
2) 2√3 : 3
3) 3√3 : 4
4) 4√3 : 3
Ответ: 3.
А6. Чему равны координаты точки А1, симметричной точке А (−2; −3) относительно прямой, заданной уравнением х = 1?
1) (4; −3)
2) (−1; −3)
3) (−3; 4)
4) (−3; −1)
Ответ: 1.
В1. Дано:
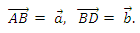
Точка Е лежит на отрезке ВС, ВЕ : ЕС = 3 : 4.
Разложите вектор
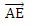
по неколлинеарным векторам
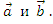
Ответ:
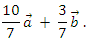
В2. В прямоугольном треугольнике АВС (угол С = 90°) медиана АМ = m проведена к меньшему катету и образует с большим катетом угол 15°. Найдите площадь треугольника.
Ответ: m2/4.
В3. Три окружности радиуса 6 см касаются друг друга. Найдите площадь криволинейного треугольника, ограниченного дугами этих окружностей.
Ответ: 36√3 − 18п см2.
В4. Напишите уравнение окружности, симметричной окружности, заданной уравнением
х2 + у2 + 8х − 6у = 0,
относительно точки А (1; 2).
Ответ: х2 + у2 − 12х − 2у − 12 = 0.
С1. Окружности радиусов 4R и 9R касаются внешним образом. К этим окружностям проведена общая касательная АВ. В криволинейный треугольник АВС (см. рис.), образованный касательной и дугами окружностей, вписана окружность. Найдите ее радиус.
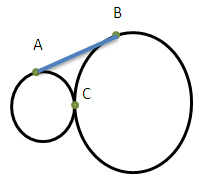
Ответ: 36/25 R.
С2. Высоты треугольника равны 3, 4 и 6. Найдите радиусы вписанной и описанной окружностей.
Ответ: 4/3 и 64/15.

