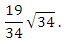А1. Напишите уравнение прямой m, симметричной прямой n, заданной уравнением х + у + 4 = 0, относительно оси у = 1.

  1) х − у + 5 = 0

  2) х − у + 3 = 0

  3) х − у + 4 = 0

  4) х − у + 6 = 0

  Ответ: 4.

 

  А2. Точка А₁ (−4; −2) симметрична точке А (2; −8)  относительно точки В. Найдите координаты центра В симметрии.

  1) (5; 1)

  2) (−5; −1)

  3) (−1; −5)

  4) (1; 5)

  Ответ: 3.

 

  А3. Определите оси симметрии графика зависимости, который задается уравнением

2Ix − 2I + 3Iy + 4I = 7.

  1) х = −2, у = 4

  2) х = 2, у = −4

  3) х = 2, у = 4

  4) х = −2, у = −4

  Ответ: 2.

 

  А4. Дан отрезок АВ с координатами концов А (−3; 4) и В (2; −1). При параллельном переносе на вектор

 

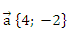
  этого отрезка получен отрезок А₁В₁. Найдите координаты концов отрезка А₁В₁.

  1) А₁ (1; 2), В₁ (−6; 3)

  2) А₁ (−1; 2), В₁ (6; −3)

  3) А₁ (−1; −2), В₁ (6; −3)

  4) А₁ (1; 2), В₁ (6; −3)

  Ответ: 4.

 

  А5. Напишите уравнение прямой m, которая получается при параллельном переносе прямой n, заданной уравнением

2х + 7у − 3 = 0,

на вектор

 

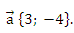
  1) 2х + 7у − 7 = 0

  2) 2х + 7у + 1 = 0

  3) 2х + 7у + 19 = 0

  4) 2х + 7у + 12 = 0

  Ответ: 3.

 

  А6. Отрезок АВ с координатами концов А (2; −3), В (−7; 1) повернут на угол 180^° вокруг начала координат и в результате этого получен отрезок А₁В₁. Найдите координаты концов этого отрезка.

  1) А₁ (2; −3), В₁ (7; −1)

  2) А₁ (−2; 3), В₁ (7; −1)

  3) А₁ (−2; 3), В₁ (−7; −1)

  4) А₁ (2; −3), В₁ (−7; −1)

  Ответ: 2.

 

  В1. Точка А₁ (−5; −1) симметрична точке А (3; −3) относительно прямой m. Напишите уравнение прямой m.

  Ответ: х − у + 2 = 0.

 

  В2. Напишите уравнение кривой, в которую переходит парабола

у = −х² + 3х + 7

  при ее отображении относительно начала координат.

  Ответ: у = х² + 3х − 7.

 

  В3. При параллельном переносе на вектор

 

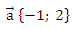
  график зависимости

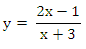
  переходит в некоторую кривую. Напишите уравнение этой кривой.

  Ответ: у = (4х + 9) / (х + 4).

 

  В4. Составьте уравнение образа окружности

х² + у² + 6х − 8у = 0

  при повороте на 270^° против часовой стрелки относительно начала координат.

  Ответ: х² + у² − 8х − 6у = 0.

 

  С1. В результате некоторого движения точка А (−3; 1) переходит в точку А₁ (9; 3), а точка В (2; −4) - в точку В₁ (4; 8). В какую точку при таком движении переходит точка С (5; −2)?

  Ответ: (1; 6).

 

  С2. Найдите расстояние между параллельными прямыми, заданными уравнениями

3х + 5у − 8 = 0 и 3х + 5у + 11 = 0.

  Ответ: