А1. Найдите сумму углов правильного семиугольника.

  1) 1260^°

  2) 1080^°

  3) 900^°

  4) 1440^°

  Ответ: 3.

 

  А2. Хорда окружности, равная а, стягивает дугу в 120^°. Найдите радиус окружности.

  1) а√3/3

  2) а√3

  3) а√3/2

  4) а√3/4

  Ответ: 1.

 

  А3. В прямоугольный треугольник с катетами, равными 5 см и 12 см, вписана окружность. Найдите ее радиус.

  1) 2,5 см

  2) 2 см

  3) 3 см

  4) 3,5 см

  Ответ: 2.

 

  А4. В окружность радиуса R вписан правильный шестиугольник. Найдите разность площадей окружности и шестиугольника.

 

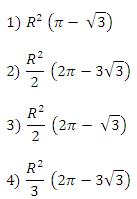
  Ответ: 2.

 

  А5. Даны две концентрические окружности. Площадь кольца, ограниченного этими окружностями, равна S. Найдите радиус меньшей окружности, если радиус большей окружности равен R.

 

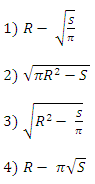
  Ответ: 3.

 

  А6. В сегмент круга радиуса R, ограниченный дугой в 90^° и стягивающей ее хордой, вписана наибольшая окружность. Найдите ее радиус.

  1) R(2 − √3)/4

  2) R(2 − √2)/4

  3) R(2 − √2)/2

  4) R(2 − √3)/2

  Ответ: 2.

 

  В1. Углы правильного многоугольника равны 156^°. Найдите число сторон этого многоугольника.

  Ответ: 15.

 

  В2. Найдите площадь сегмента, ограниченного хордой и дугой в 60^°, если радиус окружности равен R.

  Ответ: R²(4п − 3√3) / 12.

 

  В3. В угол вписаны две окружности, которые касаются сторон угла и друг друга. Отношение площадей соответствующих кругов равно 17 + 12√2. Найдите величину угла.

  Ответ: 90^°.

 

  В4. Общей хордой двух кругов стягиваются дуги в 60^° и 90^°. Найдите отношение площадей этих кругов.

  Ответ: 2 : 1.

 

  С1. В равнобедренном треугольнике основание равно 24 см, а боковая сторона равна 13 см. Найдите радиусы вписанной и описанной окружностей и расстояние между их центрами.

  Ответ: 12/5 и 169/10, 143/10.

 

  С2. Три одинаковых круга касаются друг друга. Площадь круга, который внутренним образом касается трех данных кругов, равна S. Найдите площадь каждого данного круга.

  Ответ: 3(7 + 4√3)S.