ОЛИМПИАДНЫЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ ПОВЫШЕННОЙ СЛОЖНОСТИ
4 КЛАСС
ВАРИАНТ 1
1. Мама Алёны старше её в 3 раза. А вместе им 48 лет. Сколько лет матери и сколько лет дочери?
Решение:
Пусть Алёне х лет. Тогда её маме - 3х лет. Зная, из условия задачи, что вместе им 48 лет, составим уравнение и решим его.
х + 3х = 48
4х = 48
х = 48/4 = 12
Выполним проверку:
х · 3 = 12 · 3 = 36
36 + 12 = 48
Ответ: 36 и 12.
2. В кошельке у Сергея 6 монет: по одной - 1-копеечная, 3-копеечная, 5-копеечная, 15-копеечная и остальные двухкопеечные. Какую сумму меньше 28 копеек нельзя набрать этими монетами?
Решение:
Сначала установим сколько у Сергея двухкопеечных монет. Их две. Затем методом перебора выясним какую сумму меньше 28 копеек нельзя набрать имеющимися в наличии монетами.
1 копейка - можно (1 копеечная монета);
2 копейки - можно (1 двухкопеечная монета);
3 копейки - можно (1 трехкопеечная монета);
4 копейки - можно (2 двухкопеечные монеты);
5 копеек - можно (1 пятикопеечная монета);
6 копеек - можно (1 пятикопеечная монета и 1 копеечная);
ну и так далее...
В результате мы получим, что нельзя набрать лишь сумму равную 14 копейкам, а все остальные варианты набираются.
Ответ: 14 копеек.
3. Разделите квадрат на 3 таких треугольника, чтобы среди них был лишь один с прямым углом.
Решение:
Нам необходимо сделать так, чтобы в результате нашего разделения квадрата на треугольники из 4 его прямых углов осталось не более одного и чтобы в результате построений не появились новые прямые углы.
Сначала отрезком по диагонали соединим два противолежащих угла квадрата, разделив его таким образом на два треугольника.
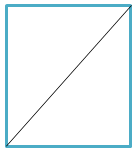
В результате мы "уничтожили" 2 прямых угла квадрата из 4, и получили 2 треугольника каждый из которых содержит по одному прямому углу. Один прямой угол мы имеем право оставить по условию задачи. А вот от второго нужно избавиться. Проведем новый отрезок из любого прямого угла к первому отрезку (но только не к его середине!). Получим, к примеру, следующее.
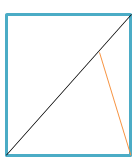
Таким образом, мы разделили квадрат на 3 треугольника, причем из них только один содержит прямой угол.
4. Марина купила в магазине набор леденцов. В первый день она съела половину всех леденцов и ещё 1. Во второй день она съела половину оставшихся леденцов и ещё 2. В третий день съела половину остатка и ещё 3. На этом все леденцы закончились. Сколько леденцов было в наборе?
Решение:
Обозначим количество леденцов в полном наборе как А. Значит в первый день было съедено (А/2) + 1. Во второй день съедена половина оставшихся и ещё 2. Но мы не знаем количество оставшихся после первого дня. Хотя можем выразить их количество в следующем виде: (А/2) − 1. Обозначим это оставшееся количество леденцов после первого дня как В. Значит во второй день Марина съела (В/2) + 2 леденцов. В третий день Марина съела половину оставшегося после второго дня и ещё 3. Причём леденцы на этом закончились. То есть половина данного остатка была равна 3. Следовательно всего после второго дня оставалось 6 леденцов.
Составим уравнение отдельно для второго дня и решим его.
Было В леденцов. Съели (В/2) + 2. Осталось 6.
В − ((В/2) + 2) = 6
В − В/2 − 2 = 6
В/2 = 8
В = 16
У нас В = (А/2) − 1.
(А/2) − 1 = 16
А/2 = 17
А = 34
Значит в полном наборе было 34 леденца.
Ответ: 34.
5. Найдите все натуральные числа, при делении которых на 7 в частном получится то же число, что и в остатке.
Решение:
Здесь нужно сообразить, что остаток не может быть больше или равным 7, так как в противном случае он тоже должен делится. А значит и максимальное возможное частное для данного условия будет равно 6. То есть частными могут быть числа 1, 2, 3, 4, 5, 6. А им соответствуют по условию задачи следующие делимые: 8; 16; 24; 32; 40; 48.
Такой же результат можно получить если подставлять последовательно в формулу 7а + а натуральные числа от единицы и более, а полученные числа делить на 7 для проверки выполнения условий задачи.
Ответ: 8, 16, 24, 32, 40, 48.
6. В классе 28 учеников. Известно, что из любых 10 учеников хотя бы 1 мальчик. Сколько девочек может быть в этом классе?
Решение:
Если из любых 10 учеников хотя бы один мальчик, значит 10 девочек в классе набрать невозможно. Следовательно, девочек в классе не более 9. Причем, девочек может не быть в этом классе вообще.
Ответ: не более 9.
7. Костя едет на велосипеде в школу со скоростью 60 км/ч. С какой скоростью ему нужно ехать, чтобы проезжать 1 км на 1/3 минуты быстрее?
Решение:
Для удобства будем считать скорость в км/сек.
60 км/ч = 60 км/3600 сек = 1 км / 60 сек
1/3 мин = 20 секунд, значит скорость должна быть 1 км / 40 секунд.
Переведем полученную скорость обратно в км/ч.
1 км / 40 сек = 90 км / 3600 сек = 90 км/ч
Ответ: 90 км/ч.

